$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$

Bloch Sphere Orthonormality

^{First created in July 2018}

Introduction

A general qubit is in the form of $\Ket{\psi}=\alpha\Ket0+\beta\Ket1$, where $\alpha$ and $\beta$ are complex numbers. Together they would have four degrees of freedom and are hard to visualise.

Physicist Felix Bloch has taken the advantage of two facts: 1) in pure state $\alpha^2+\beta^2=1$, and 2) phase is relative, and created a two dimensional sphere to represent a qubit.

The first fact gives us unit length vectors, so all possible values of $(\alpha,\beta)$ are on a 4D sphere.

Secondly, since phase is relative, we can make $\alpha$, the coefficient of $\Ket0$, real and non-negative.

That will reduce the state space $(\alpha,\beta)$ to a 3D sphere, which is called a Bloch Sphere.

Please note that the two state bases $\Ket0$ and $\Ket1$ are orthonormal. But on the Bloch Sphere, they are presented as two opposite ends of the same axis.

Any states on the Bloch Sphere can be represented by $~\boxed{\Ket{\psi}=\cos\frac{\theta}{2}\Ket0+e^{i\phi}\sin\frac{\theta}{2}\Ket1}$,\qquad where $\theta\in[0,\pi]$ and $\phi\in[0,2\pi)$.

Bloch vs Hilbert

Let us see how to visualise the transition from a Hilbert space sphere with a orthonormal basis $\{\Ket0, \Ket1\}$, into the Bloch Sphere with these two states at the North Pole and South Pole respectively.

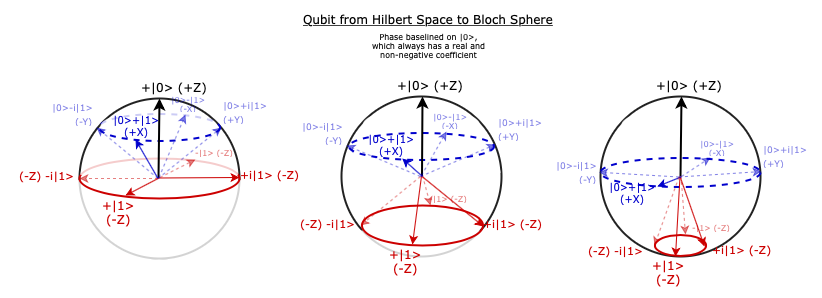
The diagrams above indicate a progressive transition from the 3D Hilbert space hemisphere (non-negative $\Ket0$) on the left into the (almost) Bloch Sphere on the right.

The X-Y plane on the Bloch Sphere corresponds to the blue cone on the Hilbert space sphere. As the red $\Ket1$ circle is moving downwards and converging into a single point in the South Pole, the blue circle comes to the equator.

Please note:

• There is no "Bloch vectors" exists in the lower semisphere on the left, as that would make the coefficient of $\Ket 0$ negative, against the Bloch Sphere restrictions.
  
  

• The four values, $+\Ket1, +i\Ket1, -\Ket1$ and $-i\Ket1$, are all at the South Pole, which is not an issue. When there is no $\Ket0$, the relative phase of $\Ket1$ is irrelevant. By convention, we will use only $+\Ket1$.
  
  

• In the Hilbert space sphere $\theta\in[0,\pi/2]$ and in Bloch Sphere $\theta\in[0,\pi]$, while $\phi\in[0,2\pi)$ remains true in both cases. The arc between the two Bloch Sphere poles is double the same arc in the Hilbert space sphere, which explains why there is a factor of $\frac{1}{2}$ on the Bloch Sphere $\theta$, but not on the $\phi$.
  
  

• What appears as perpendicular lines in the Hilbert Space diagram above may not correspond to orthonomal vectors.
  e.g. $\Rsr2\left(\Ket0+\Ket1\right)$ and $i\Ket1$ are not orthonomal, even they appear to be perpendicular.

Orthonormality

As you see, the orthonormal basis vectors $\Ket0$ and $\Ket1$ are transformed into the $Z$-axis with the two vectors at each end of the axis. Is it true that any pair of arbitrary orthonormal vectors present themselves as the two opposite ends of a diameter on the Bloch Sphere?

This statement is true for all three Pauli axes. The two ends of them are orthonormal.

1. $X$-axis, $\Rsr2(\Bra0-\Bra1)\Rsr2(\Ket0+\Ket1)=0$,
2. $Y$-axis, $\Rsr2(\Bra0-i\Bra1)\Rsr2(\Ket0+i\Ket1)=0$, and
3. $Z$-axis, $\Braket{1\Verti 0}=0$.

---

The two ends of a diameter on the Bloch Sphere represent two orthogonal states.

Proof:

For an arbitrary vector $\Ket\psi=\cos\theta/2\Ket0+e^{i\phi}\sin\theta/2\Ket1$, its Bloch vector (projection of $\Ket\psi$ on the three Pauli axes) is $\HAT\psi=(\cos\phi\sin\theta,\sin\phi\sin\theta,\cos\theta)$.

The "opposite end" $\HAT{\psi'}$ would have $\theta'=\pi-\theta$ and $\phi'=\pi+\phi$.

To verify that $\HAT\psi$ and $\HAT{\psi'}$ are orthonormal,

$\HAT{\psi'}=(\cos\phi'\sin\theta',\sin\phi'\sin\theta',\cos\theta')\\ =(\cos(\pi+\phi)\sin(\pi-\theta),\sin(\pi+\phi)\sin(\pi-\theta),\cos(\pi-\theta))\\ =(-\cos\phi\sin\theta,-\sin\phi\sin\theta,-\cos\theta),\text{ which makes sense}.$

$\Ket{\psi'} =\cos\theta'/2\Ket0+e^{i\phi'}\sin\theta'/2\Ket1 =\cos(\pi-\theta)/2\Ket0+e^{i(\pi+\phi)}\sin(\pi-\theta)/2\Ket1 .$

$\Bra{\psi'} =\sin(\theta/2)\Bra0+e^{i(\pi-\phi)}\cos(\theta/2)\Bra1 .$

$\Braket{\psi'\Verti\psi} =\sin(\theta/2)\cos(\theta/2)+e^{i(\pi-\phi)}\cos(\theta/2)e^{i\phi}\sin(\theta/2)\\ =\cos(\theta/2)\sin(\theta/2)-\cos(\theta/2)\sin(\theta/2) =0 .$

This confirms that the two ends of an arbitrary diameter on the Bloch Sphere are orthonormal in Hilbert Space.

---

Two orthogonal states are at the opposite ends on a Bloch Sphere diameter.

Proof:

To prove the converse, that two orthonormal states in the Hilbert Space are at the two ends of a diameter on the Bloch Sphere, let us found the general form of an orthonormal state.

Let $\Ket\psi=\cos\theta/2\Ket0+e^{i\phi}\sin\theta/2\Ket1$, $\Ket{\psi'}=\cos\theta'/2\Ket0+e^{i\phi'}\sin\theta'/2\Ket1$ and $\Ket{\psi'}$ is orthonormal to $\Ket\psi$.

$\Braket{\psi'\Verti\psi} =\cos(\theta/2)\cos(\theta'/2)+e^{i(\phi-\phi')}\sin(\theta/2)\sin(\theta'/2)\\ ={1\over2}(\cos(\theta+\theta')/2+\cos((\theta-\theta')/2) -e^{i(\phi-\phi')}{1\over2}(\cos(\theta+\theta')/2-\cos((\theta-\theta')/2)\\ =0.$

i.e. $\left(\cos(\theta+\theta')/2+\cos((\theta-\theta')/2\right) =e^{i(\phi-\phi')}\left(\cos(\theta+\theta')/2-\cos(\theta-\theta')/2\right) .$

Since the LHS is real, $e^{i(\phi-\phi')}$ must be real, and the only possible values are $\pm1$. Bear in mind at all time that $\theta,\theta'\in[0,\pi]$ and $\phi,\phi'\in[0,2\pi)$.

$\begin{array}{|c|c|c|c|c|c|} \hline e^{i(\phi-\phi')} & \phi-\phi' & \phi' & \text{Step 1} & \text{Step 2} & \theta' \\ \hline +1 & 0,2\pi & \phi & \cos(\theta-\theta')/2=0 & \theta-\theta'=\pm\pi & \theta\pm\pi \\ \hline -1 & \pi,3\pi & \phi-\pi & \cos(\theta+\theta')/2=0 & \theta+\theta'=\pi & \pi-\theta \\ \hline \end{array}$

$\left\{ \begin{array}{lll} \text{Case }+1 & \ldots & \phi'=\phi,~~\theta'=\theta\pm\pi,~~(\theta,\theta')=(0,\pi)\text{ or }(\pi,0).\\ \text{Case }-1 & \ldots & \phi'=\phi-\pi,~~\theta'=\pi-\theta. \end{array} \right.$

In both cases, $\Ket\psi$ and $\Ket{\psi'}$ are at the opposite ends on a Bloch Sphere diameter.