$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$

Kous Octant Visualisation

^{First created in June 2018}

This page is to provide a mind model to imagine the effect of various operators on a qubit by means of rubiks-cube-like rotations on the Bloch Sphere.

The $\pi/4$ table would help you mentally verify quantum gate operations.

Note: There are other ways to visualise an operator $O$. For example, noting the relative position of $\Ket\psi$ with the $Z$-$X$ frame (or any orthogonal 2-vector frame easy for you), rotating the frame based on $O$, and afterwards locating the new $O\Ket\psi$ in relation to the rotated frame $OZ$-$OX$.

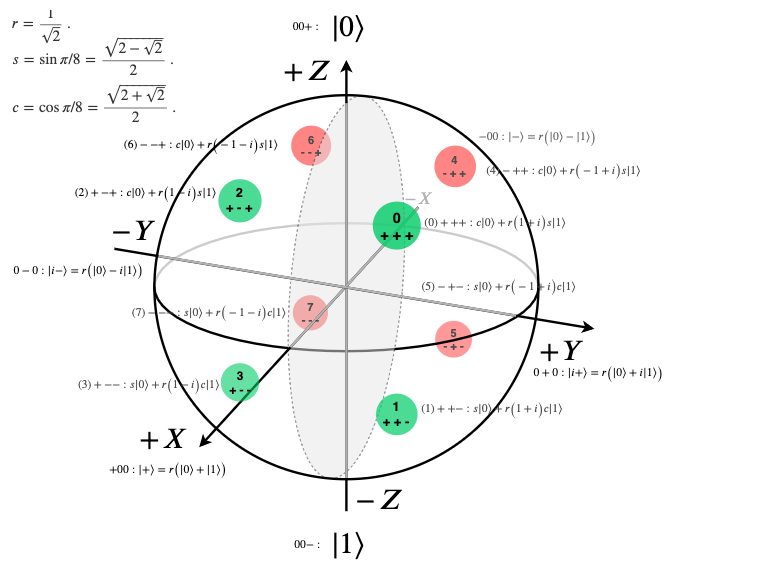
The "Octant Vector"

One way to visualise state vector rotations about an axis is to use the "octant vector", which is in the "centre" of each octant of the Bloch Sphere:

$\displaystyle \cos(\theta/2)\Ket{0}+e^{i\phi}\sin(\theta/2)\Ket{1} =\cos(\theta/2)\Ket{0}+(\cos\phi+i\sin\phi)\sin(\theta/2)\Ket{1} .$

$\displaystyle s_4 =\sin\pi/4=\Rsr2~,~~ c_4 =\cos\pi/4=\Rsr2~,~~ s_8 =\sin\pi/8 =\frac{\sqrt{2-\sqrt2}}{2}~,~~ c_8 =\cos\pi/8 =\frac{\sqrt{2+\sqrt2}}{2} .$

$\displaystyle \sin{\pi/8}=s_8,~~ \sin{3\pi/8}=c_8,~~ \cos{\pi/8}=c_8,~~ \cos{3\pi/8}=s_8~ .$

$\displaystyle \text{Let }r_2=\Rsr2,~~ s_4=c_4=r_2~ .$

$\displaystyle \cos{\pi/4}=r_2,~~ \cos{3\pi/4}=-r_2,~~ \cos{5\pi/4}=-r_2,~~ \cos{7\pi/4}=r_2~ .$

$\displaystyle \sin{\pi/4}=r_2,~~ \sin{3\pi/4}=r_2,~~ \sin{5\pi/4}=-r_2,~~ \sin{7\pi/4}=-r_2,~~ .$

---

$\displaystyle \text{Let }r=\Rsr2,~~ s =\sin\pi/8 =\frac{\sqrt{2-\sqrt2}}{2}~,~~ c =\cos\pi/8 =\frac{\sqrt{2+\sqrt2}}{2}.~~ \text{Also, }~r=2sc .$

Octant centred vector	$X$	$Y$	$Z$	#	\hspace{1em}$\theta/2$\hspace{1em}	\hspace{2em}$\phi$\hspace{2em}	\hspace{1em}$\Ket0$\hspace{1em}	\hspace{5em}$\Ket1$\hspace{5em}
$\frac{1}{\sqrt 3}[1,1,1]^T$	+	+	+	0	$\pi/8$	$\pi/4$	$c$	$r~(1+i)~s$
$\frac{1}{\sqrt 3}[1,1,-1]^T$	+	+	-	1	$3\pi/8$	$\pi/4$	$s$	$r~(1+i)~c$
$\frac{1}{\sqrt 3}[1,-1,1]^T$	+	-	+	2	$\pi/8$	$7\pi/4$	$c$	$r~(1-i)~s$
$\frac{1}{\sqrt 3}[1,-1,-1]^T$	+	-	-	3	$3\pi/8$	$7\pi/4$	$s$	$r~(1-i)~c$
$\frac{1}{\sqrt 3}[-1,1,1]^T$	-	+	+	4	$\pi/8$	$3\pi/4$	$c$	$r~(-1+i)~s$
$\frac{1}{\sqrt 3}[-1,1,-1]^T$	-	+	-	5	$3\pi/8$	$3\pi/4$	$s$	$r~(-1+i)~c$
$\frac{1}{\sqrt 3}[-1,-1,1]^T$	-	-	+	6	$\pi/8$	$5\pi/4$	$c$	$r~(-1-i)~s$
$\frac{1}{\sqrt 3}[-1,-1,-1]^T$	-	-	-	7	$3\pi/8$	$5\pi/4$	$s$	$r~(-1-i)~c$

Examples:

$X\big(c\Ket0+r~(1+i)~s\Ket1\big) =c\Ket1+r~(1+i)~s\Ket0 \sim r~(1-i)\big(c\Ket1+r~(1+i)~s\Ket0\big) =s\Ket0+r~(1-i)~c\Ket1 .$

$Y\big(c\Ket0+r~(1+i)~s\Ket1\big) =ic\Ket1-ir~(1+i)~s\Ket0 \sim r~(1+i)\big(ic\Ket1+r~(1-i)~s\Ket0\big) =s\Ket0+r~(-1+i)~c\Ket1 .$

$Z\big(c\Ket0+r~(1+i)~s\Ket1\big) =c\Ket0+r~(-1-i)~s\Ket1 .$

The $\pi/4$ Table

This table covers all possible rotations from octant-centred vectors anti-clockwise by $\pi/2$. (It corresponds to the six rotation stacks on a 2x2 rubik's cube.)

Axis	First	Second	Third	Fourth
$X$	0	2	3	1
$Y$	0	1	5	4
$Z$	0	4	6	2
$X$	7	5	4	6
$Y$	7	6	2	3
$Z$	7	3	1	5

To rotate $\pi$ about any axes (jumping two columns) can be visualised as drawing an arc on the surface of the Bloch Sphere from the starting vector reaching the axis vector (either head or tail), extending the same arc an equal length, and arriving at the resulting vector.

If you want to go "under the surface", you can draw a straight line from the starting vector perpendicular to the rotation axis and extend that line to reach the resulting vector.

Example: You can use $\sqrt Z\sqrt X\sqrt Z$ to implement a Hadamard gate, which has the following map:

$\Ket\psi$	H	$\sqrt Z$	$\sqrt X\sqrt Z$	$\sqrt Z\sqrt X\sqrt Z$
0	2	4	6	2
1	6	5	4	6
2	0	0	2	0
3	4	1	0	4
4	3	6	7	3
5	7	7	5	7
6	1	2	3	1
7	5	3	1	5

As you see, column $H$ and the last match.

Also, $H=U(\pi/2,0,\pi)=R_y(\pi/2)R_z(\pi).$

$\Ket\psi$	H	$R_z(\pi)$	$R_y(\pi/2)R_z(\pi)$
0	2	6	2
1	6	7	6
2	0	4	0
3	4	5	4
4	3	2	3
5	7	3	7
6	1	0	1
7	5	1	5

Again, $H$ and last column match, so $H=\sqrt Y~Z$. You get the idea.