$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$

IBM Q - Sqrt T

^{First created in August 2018}

The challenge from the IBM Q Experience - Basic Circuit Identities and Larger Circuits page is

Arbitrarily good approximations exist, so can you find a better one? How might you use these circuits to construct an approximate controlled-$T$ unitary transformation?

This page will answer the two challenges, followed by some illustration through programming.

Preamble

# Preamble
import numpy as np
import math
import matplotlib.pyplot as plt

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute
from qiskit.tools.visualization import plot_histogram, plot_state, plot_bloch_vector, circuit_drawer

from IPython.display import Math
# e.g. Math('3 \cdot \\frac{\pi}{2} + e^{\\frac{I*x}{x^2 + y}}')
# m = Math(...)
# display(m)

shots = 1024
decimals = 4

def run_job(qc_run, shots=shots):
    job = execute(qc_run, backend = 'local_qasm_simulator', shots=shots)
    result = job.result()
    data = result.get_counts(qc_run)
    for i in range(8):
        dataIndex = str(bin(i+8))[-3:]
        try:
            p = data[dataIndex]/shots
            print("P%s=%.3f" % (dataIndex, p))
        except:
            p = 0

    plot_histogram(job.result().get_counts(qc_run))
    return job


# Normalise
def normal_vec(vec):
    ret = np.copy(vec)
    vc = np.conj(ret[0])
    ret[0] = np.multiply(ret[0], vc)
    ret[1] = np.multiply(ret[1], vc)
    vec_norm = np.sqrt(np.square(np.abs(ret[0]))+np.square(np.abs(ret[1])))
    ret[0] = np.divide(ret[0], vec_norm)
    ret[1] = np.divide(ret[1], vec_norm)
    return ret


# Vector length is arbitrary.
precDP = 3  # Precision is 3 decimal places
tooSmallIgnored = 1E-5  # ignored if under 10^(-5)
def print_vec(vec):
    vecLen = len(vec)
    qbCount = int(math.log(vecLen, 2))

    vecRnd = np.around(vec, precDP)  # 3 decimal points
    jn = ''
    for i in range(vecLen):
        ket = str(bin(i+vecLen))[-qbCount:]
        if np.abs(vecRnd[i]) >= tooSmallIgnored:  # 3 decimal points
            print("%s%s|%s>" % (jn, vecRnd[i], ket), end='')
            jn = ' + '

    print()
    return vecRnd


# Find the Bloch Vector and return an array of <X>, <Y> and <Z>
def bloch_vector(qc, q, c, decimals=decimals):
    # Meaasurement circuits
    meas_x = QuantumCircuit(q, c)
    meas_x.barrier()
    meas_x.h(q)
    meas_x.measure(q, c)

    meas_y = QuantumCircuit(q, c)
    meas_y.barrier()
    meas_y.s(q).inverse()
    meas_y.h(q)
    meas_y.measure(q, c)

    meas_z = QuantumCircuit(q, c)
    meas_z.barrier()
    meas_z.measure(q, c)

    # Bloch Vector to return
    bloch = [0, 0, 0]
    
    # 3 circuits to measure X, Y and Z
    circuits = []
    circuits.append(qc + meas_x)
    circuits.append(qc + meas_y)
    circuits.append(qc + meas_z)

    # Run them all
    job = execute(circuits, backend = 'local_qasm_simulator', shots=shots)
    result = job.result()

    # Get the measurement
    for bloch_index in range(3):
        data = result.get_counts(circuits[bloch_index])
        #print(data)
        try:
            p0 = data['0']/shots
        except KeyError:
            p0 = 0
        try:
            p1 = data['1']/shots
        except KeyError:
            p1 = 0
        bloch[bloch_index] = np.round(p0 - p1, decimals)

    return bloch

def bloch_angles(bv, show="", decimals=decimals):
    (x, y, z) = bv
    # cos(theta)=z; theta in [-1, 1]
    if (z > 1):
        z = 1.0
    elif (z < -1):
        z = -1.0
    theta = np.arccos(z)
    # Projection on x-y in [0, 1]
    xy = np.sin(theta)
    phi = 0.0
    if (xy > 0):
        # phi in [0, pi]
        cosphi = x/xy
        if (cosphi > 1):
            cosphi = 1.0
        elif (cosphi < -1):
            cosphi = -1.0
        phi = np.arccos(cosphi)
        if (y < 0 and phi > 0):
            phi = np.pi * 2 - phi

    theta = np.round(theta, decimals)
    phi = np.round(phi, decimals)

    thetaPI = str(np.round(theta/np.pi, decimals))
    thetaPI2 = str(np.round(theta/np.pi/2, decimals))
    phiPI = str(np.round(phi/np.pi, decimals))

    if (show == "pi"):
        return thetaPI + "pi, " + phiPI + "pi"
    elif (show == "math"):
        return Math("\cos(" + thetaPI2 + "\pi)\Ket0 + e^{i~" + phiPI + "\pi}\sin(" + thetaPI2 + "\pi)\Ket1")
    elif (show == "pion"):
        thetaPIon = "pi/" + str(np.round(np.pi/theta, 2))
        phiPIon = "pi/" + str(np.round(np.pi/phi, 2))
        return thetaPIon + ", " + phiPIon
    else:
        return [theta, phi]
    

Trial Circuit

$\large\sqrt T\Ket0=\cos{\pi\over4}\Ket0+e^{i\pi/8}\sin{\pi\over4}\Ket1 \approx 0.7071\Ket0+(0.6533+i~0.2706)\Ket1 .$

Bloch Vector: $\large\left(\sqrt{2+\sqrt2},\sqrt{2-\sqrt2},0\right)\approx(0.92388,0.38268,0)$

$Q=HTHTHSTHTHSTHTHTH$.

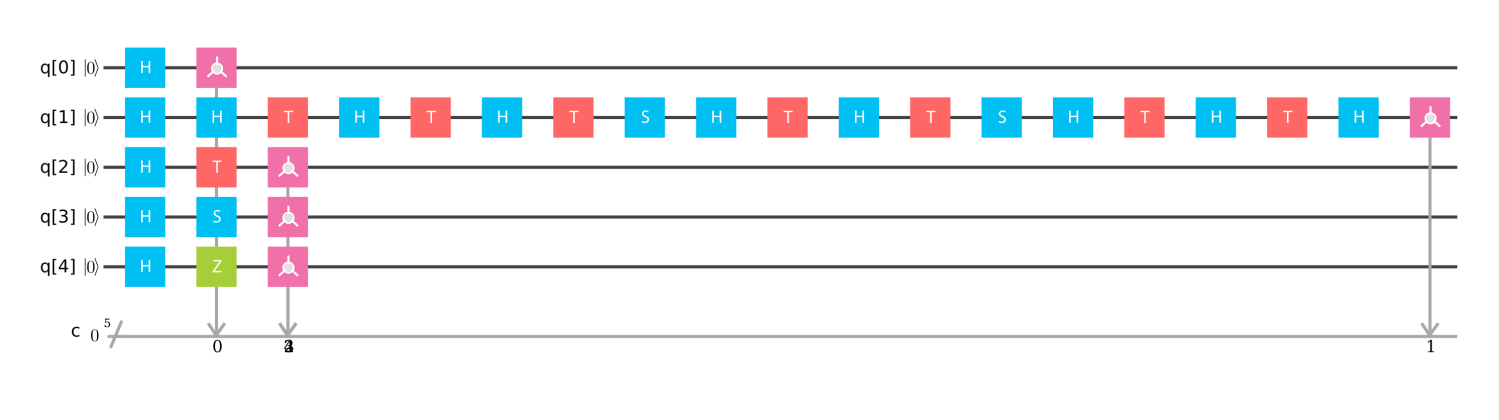
# Number of qubits
qbNum = 1

# Define the Quantum and Classical Registers
q = QuantumRegister(qbNum)
c = ClassicalRegister(qbNum)

qc = QuantumCircuit(q, c)

# Bloch Vector expected
bloch_expected = [0.92388, 0.38268, 0]
# Preparation
qc.h(q)

# Build
qc.h(q)
qc.t(q)
qc.h(q)
qc.t(q)
qc.h(q)
qc.t(q)
qc.s(q)
qc.h(q)
qc.t(q)
qc.h(q)
qc.t(q)
qc.s(q)
qc.h(q)
qc.t(q)
qc.h(q)
qc.t(q)
qc.h(q)

# Circuit building
# ...

# Finalisation
# ...

shots = 8192

# State Vector
job = execute(qc, backend = 'local_statevector_simulator', shots=shots)
data = np.round(job.result().get_statevector(qc), decimals)
print("Raw vector:", end=" ")
print(data)
vec_norm = np.round(normal_vec(data), decimals)
print("Normalised:", end=" ")
print(vec_norm)
print("Ket form:  ", end=" ")
print_vec(vec_norm)
print()

# Block Vector
bloch = bloch_vector(qc, q, c)
print("Bloch Vector:")
print("Expected:", end=" ")
print(np.round(bloch_expected, decimals))
print("Measured:", end=" ")
print(np.round(bloch, decimals))
print("M-E:     ", end=" ")
print(np.round(np.subtract(bloch, bloch_expected), decimals))
print("M/E-100%:", end=" ")
#print("%s %f%% on x, %f%% on y" %
#      (np.round(bloch, decimals), \
#       np.round((bloch[0]/bloch_expected[0]-1)*100, decimals+2), \
#       np.round((bloch[1]/bloch_expected[1]-1)*100, decimals+2)))
#print(np.subtract(np.round(bloch, decimals), np.round(bloch_expected, decimals)))
print("%f%%" % np.round((bloch[0]/bloch_expected[0]-1)*100, decimals+2), end=" ")
print("%f%%" % np.round((bloch[1]/bloch_expected[1]-1)*100, decimals+2), end=" n/a")
print()
#print(bloch_angles(bloch, show="pi"))
display(bloch_angles(bloch, show="math", decimals=3))

plot_bloch_vector(bloch)

# Histogram
#qc.measure(q, c)
#job = execute(qc, backend = 'local_qasm_simulator', shots=shots)
#data = job.result().get_counts(qc)
#plot_histogram(data)

# Check the circuit (must be last or it will not show)
#circuit_drawer(qc)

Raw vector: [0.4268+0.5732j 0.1768+0.6768j]
Normalised: [0.7146+0.j     0.6484+0.2624j]
Ket form:   (0.715+0j)|0> + (0.648+0.262j)|1>

Bloch Vector:
Expected: [0.9239 0.3827 0.    ]
Measured: [0.928  0.4006 0.0186]
M-E:      [0.0041 0.0179 0.0186]
M/E-100%: 0.445945% 4.682764% n/a

$$\cos(0.247\pi)\Ket0 + e^{i~0.121\pi}\sin(0.247\pi)\Ket1$$

bvmax = 0.0
showWhat = ""
bvLastStr = ""

def bloch_step(op, cap="Initial State"):
    global stepNum, bvmax, bvLastStr
    stepNum += 1
    print("Step %d: %s" % (stepNum, cap))
    op(q)

    # Ket Form
    job = execute(qc, backend = 'local_statevector_simulator', shots=shots)
    data = np.round(job.result().get_statevector(qc), decimals)
    bv = bloch_vector(qc, q, c)
    
    # Normalised Vector
    vec_norm = np.round(normal_vec(data), decimals)
    print_vec(vec_norm)

    # Math
    display(bloch_angles(bv, show="math", decimals=3))

    # Theta and Phi
    print(bloch_angles(bv, show="pi"))

    # Bloch Vector with max
    if (bvLastStr != ""):
        print("%s: %s" % (cap, bvLastStr), end=" -> ")
    print(bv, end=" max=")
    bvmax = np.amax(bv)
    print(bvmax)
    bvLastStr = bv
    
    # Bloch Sphere
    plot_bloch_vector(bv)

    bvLast = bv

approxNum = 0

def bloch_approx():
    global approxNum
    approxNum += 1
    print("Approximation %d: max=%f\n\n" % (approxNum, bvmax))

def sqrtT():
    #bloch_step(qc.iden, "I")
    bloch_step(qc.iden)
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T Marked")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T")
    bloch_step(qc.s, "S")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T Marked")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T")
    bloch_step(qc.s, "S")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T Marked")
    bloch_step(qc.h, "H")
    bloch_step(qc.t, "T")
    bloch_step(qc.h, "H Final")

qbNum = 1

q = QuantumRegister(qbNum)
c = ClassicalRegister(qbNum)

qc = QuantumCircuit(q, c)

stepNum = -1
shots = 8192

# Initial state -> Final state
# Ket0 -> Ket0
#sqrtT()

# Ket+ -> Ket0+e^{i pi/4}Ket1
qc.h(q)
sqrtT()

Step 0: Initial State
(0.707+0j)|0> + (0.707+0j)|1>

$$\cos(0.251\pi)\Ket0 + e^{i~0.0\pi}\sin(0.251\pi)\Ket1$$

0.5024pi, 0.0pi
[1.0, 0.0078, -0.0076] max=1.0

Step 1: H
(1+0j)|0>

$$\cos(0.0\pi)\Ket0 + e^{i~0.0\pi}\sin(0.0\pi)\Ket1$$

0.0pi, 0.0pi
H: [1.0, 0.0078, -0.0076] -> [0.0007, 0.0098, 1.0] max=1.0

Step 2: T
(1+0j)|0>

$$\cos(0.0\pi)\Ket0 + e^{i~0.0\pi}\sin(0.0\pi)\Ket1$$

0.0pi, 0.0pi
T: [0.0007, 0.0098, 1.0] -> [0.0242, 0.0049, 1.0] max=1.0

Step 3: H
(0.707+0j)|0> + (0.707+0j)|1>

$$\cos(0.249\pi)\Ket0 + e^{i~0.0\pi}\sin(0.249\pi)\Ket1$$

0.4985pi, 0.0pi
H: [0.0242, 0.0049, 1.0] -> [1.0, 0.0007, 0.0046] max=1.0

Step 4: T Marked
(0.707+0j)|0> + (0.5+0.5j)|1>

$$\cos(0.247\pi)\Ket0 + e^{i~0.25\pi}\sin(0.247\pi)\Ket1$$

0.4947pi, 0.2502pi
T Marked: [1.0, 0.0007, 0.0046] -> [0.7065, 0.6934, 0.0166] max=0.7065

Step 5: H
(0.924+0j)|0> + (-0-0.383j)|1>

$$\cos(0.127\pi)\Ket0 + e^{i~1.511\pi}\sin(0.127\pi)\Ket1$$

0.2545pi, 1.5114pi
H: [0.7065, 0.6934, 0.0166] -> [0.0256, -0.7178, 0.697] max=0.697

Step 6: T
(0.924+0j)|0> + (0.271-0.271j)|1>

$$\cos(0.126\pi)\Ket0 + e^{i~1.749\pi}\sin(0.126\pi)\Ket1$$

0.2521pi, 1.749pi
T: [0.0256, -0.7178, 0.697] -> [0.5017, -0.4976, 0.7024] max=0.7024

Step 7: S
(0.924+0j)|0> + (0.271+0.271j)|1>

$$\cos(0.127\pi)\Ket0 + e^{i~0.242\pi}\sin(0.127\pi)\Ket1$$

0.2534pi, 0.2424pi
S: [0.5017, -0.4976, 0.7024] -> [0.5173, 0.4858, 0.6995] max=0.6995

Step 8: H
(0.866+0j)|0> + (0.408-0.289j)|1>

$$\cos(0.169\pi)\Ket0 + e^{i~1.79\pi}\sin(0.169\pi)\Ket1$$

0.3371pi, 1.7906pi
H: [0.5173, 0.4858, 0.6995] -> [0.6899, -0.4949, 0.4897] max=0.6899

Step 9: T Marked
(0.866+0j)|0> + (0.493+0.085j)|1>

$$\cos(0.167\pi)\Ket0 + e^{i~0.039\pi}\sin(0.167\pi)\Ket1$$

0.3333pi, 0.0394pi
T Marked: [0.6899, -0.4949, 0.4897] -> [0.8594, 0.1555, 0.5] max=0.8594

Step 10: H
(0.963+0j)|0> + (0.26-0.076j)|1>

$$\cos(0.086\pi)\Ket0 + e^{i~1.934\pi}\sin(0.086\pi)\Ket1$$

0.1718pi, 1.9343pi
H: [0.8594, 0.1555, 0.5] -> [0.5029, -0.1582, 0.8579] max=0.8579

Step 11: T
(0.963+0j)|0> + (0.237+0.13j)|1>

$$\cos(0.087\pi)\Ket0 + e^{i~0.147\pi}\sin(0.087\pi)\Ket1$$

0.1731pi, 0.1472pi
T: [0.5029, -0.1582, 0.8579] -> [0.4631, 0.2437, 0.8557] max=0.8557

Step 12: S
(0.963+0j)|0> + (-0.13+0.237j)|1>

$$\cos(0.085\pi)\Ket0 + e^{i~0.662\pi}\sin(0.085\pi)\Ket1$$

0.1695pi, 0.6618pi
S: [0.4631, 0.2437, 0.8557] -> [-0.2471, 0.4519, 0.8616] max=0.8616

Step 13: H
(0.612+0j)|0> + (0.697-0.373j)|1>

$$\cos(0.291\pi)\Ket0 + e^{i~1.841\pi}\sin(0.291\pi)\Ket1$$

0.5823pi, 1.8409pi
H: [-0.2471, 0.4519, 0.8616] -> [0.8486, -0.4475, -0.2556] max=0.8486

Step 14: T Marked
(0.612+0j)|0> + (0.757+0.229j)|1>

$$\cos(0.291\pi)\Ket0 + e^{i~0.095\pi}\sin(0.291\pi)\Ket1$$

0.5826pi, 0.0947pi
T Marked: [0.8486, -0.4475, -0.2556] -> [0.9241, 0.3003, -0.2566] max=0.9241

Step 15: H
(0.982+0j)|0> + (-0.127-0.143j)|1>

$$\cos(0.06\pi)\Ket0 + e^{i~1.272\pi}\sin(0.06\pi)\Ket1$$

0.1195pi, 1.2716pi
H: [0.9241, 0.3003, -0.2566] -> [-0.241, -0.2749, 0.9304] max=0.9304

Step 16: T
(0.982+0j)|0> + (0.011-0.191j)|1>

$$\cos(0.061\pi)\Ket0 + e^{i~1.503\pi}\sin(0.061\pi)\Ket1$$

0.1218pi, 1.5032pi
T: [-0.241, -0.2749, 0.9304] -> [0.0037, -0.3796, 0.9277] max=0.9277

Step 17: H Final
(0.715+0j)|0> + (0.648+0.262j)|1>

$$\cos(0.249\pi)\Ket0 + e^{i~0.128\pi}\sin(0.249\pi)\Ket1$$

0.4977pi, 0.1284pi
H Final: [0.0037, -0.3796, 0.9277] -> [0.9197, 0.3787, 0.0073] max=0.9197

Let us take the transformation step by step, and imagine what $\Ket0$ would do under the same transformation.

Nothing seems to have happened at step 3, but if you look at $\Ket0$ in terms of ($\theta,\phi$), it went from the initial state $(0,0)$ to H1:$(\pi/2,0)$, T2:$(\pi/2,\pi/4)$, to H3:$(\pi/4,3\pi/2)$.

Following the sequence, the final state H17 would see $\Ket0$ back to itself, which is required.

---

Now back to $\Ket+$ or $(\pi/2,0)$. If we subject $\Ket\psi=\cos\theta/2\Ket0+e^{i\phi}\sin\theta/2\Ket1\mapsto(\theta,\phi)$ to the three gates $T$, $S$ and $H$, the results are:

$T\Ket\psi=(\theta,~\phi+\pi/4).~~~ S\Ket\psi=(\theta,~\phi+\pi/2) .$

With $H$, it is easier to use the Bloch Vector presentation.

$\Ket\psi=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta).~~ H\Ket\psi=(\cos\theta,-\sin\theta\sin\phi,\sin\theta\cos\phi) .$

In short, after $H$, $\Braket{X}$ and $\Braket{Z}$ swap and $\Braket{Y}$ negated.

---

KETP

---

$H\Ket\psi =\cos\theta/2\Rsr2(\Ket0+\Ket1)+e^{i\phi}\sin\theta/2\Rsr2(\Ket0-\Ket1) =\Rsr2\left((\cos\theta/2+e^{i\phi}\sin\theta/2)\Ket0+(\cos\theta/2-e^{i\phi}\sin\theta/2)\Ket1\right) .$