$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$
Stern-Gerlach Experiment¶
First created in September 2018
The Stern-Gerlach Experiment in 1922 was the first illustration of the existance of a 2-state qubit. The experiment was to measure electron spin along two verticle axis.
To mask the technical complication, the colour of black and white and the hardness of hard and soft are used in the narative instead of electron spin.
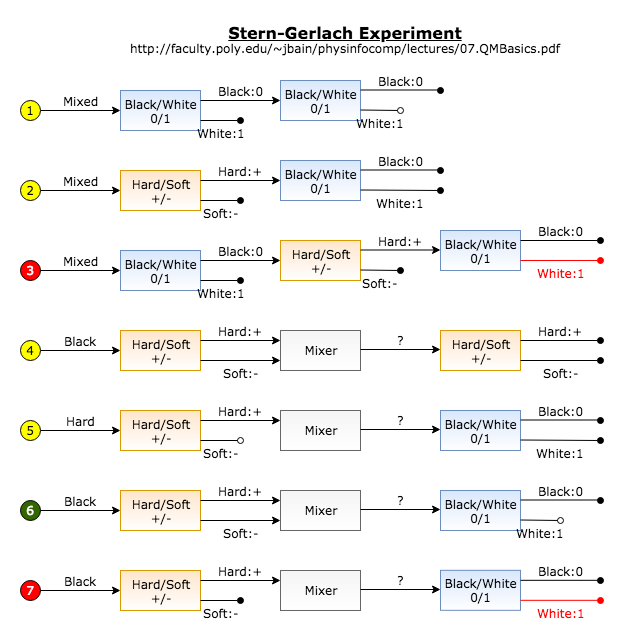
In the above illustration of the Stern-Gerlach experiment, one may interpret Black and White being $\Ket0$ and $\Ket1$, and Hard and Soft being $\Ket+$ and $\Ket-$.
There might be a misperception that basis $\{\Ket0,\Ket1\}$ is more foundamental than $\{\Ket+,\Ket-\}$, as $\Ket+=\Rsr2(\Ket0+\Ket1)$ gives an impression that $\Ket+$ is composite. If one look at $\Ket0=\Rsr2(\Ket++\Ket-),$ one would see that the two bases are in equal footing.
Another example can be found in the YouTube video (in Ref) using photon polarisation. This is a more comprehensive illustration including phase shift and linear combination.