$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$
Rotation - Matrix Exponential¶
First created in September 2018
Matrix exponential is a big topic and here only the aspect useful for quantum computing are discussed.
Definition: $\displaystyle e^A=\sum_{k=0}^\infty{1\over k!}A^k$
Properties¶
$e^\mathbb{0}=I,~~~$as the only non-trivial term is $I$ (when $k=0$) and all other terms become zero.
$e^{\alpha I}=\sum_{k=0}^\infty{1\over k!}(\alpha I)^k=e^\alpha I.$
$e^{A^T}=\left(e^A\right)^T,~~~$ as $\sum_{k=0}^\infty{1\over k!}\left(A^T\right)^k=\left(\sum_{k=0}^\infty{1\over k!}A^k\right)^T.$
$e^{A^\dagger}=\left(e^A\right)^\dagger,~~~$ as $\sum_{k=0}^\infty{1\over k!}\left(A^\dagger\right)^k=\left(\sum_{k=0}^\infty{1\over k!}A^k\right)^\dagger.$
$e^{BAB^{-1}}=B~e^A~B^{-1},~~~$ as $\sum_{k=0}^\infty{1\over k!}(BAB^{-1})^k=B\left(\sum_{k=0}^\infty{1\over k!}A^k\right)B^{-1}.$
$Ae^{\alpha A}=e^{\alpha A}A.~~~$ i.e. $[A,e^{\alpha A}]=0.$
If $AB=BA,~~e^Ae^B=e^{A+B}.$
Proof: Since $A$ and $B$ commute, $(A+B)^k=\left(\sum_{r=0}^k\frac{k!}{(k-r)!r!}A^{k-r}B^r\right).$
$\displaystyle e^{A+B} =\sum_{k=0}^\infty{1\over k!}(A+B)^k =\sum_{k=0}^\infty{1\over k!}\left(\sum_{r=0}^k\frac{k!}{(k-r)!r!}A^{k-r}B^r\right) =\sum_{k=0}^\infty\left(\sum_{r=0}^k\frac{A^{k-r}}{(k-r)!}\cdot\frac{B^r}{r!}\right)\\ \displaystyle =\sum_{r=0}^\infty\left(\sum_{k=r}^\infty\frac{A^{k-r}}{(k-r)!}\cdot\frac{B^r}{r!}\right) =\sum_{r=0}^\infty\frac{B^r}{r!}\left(\sum_{k=r}^\infty\frac{A^{k-r}}{(k-r)!}\right) =\sum_{r=0}^\infty\frac{B^r}{r!}\left(\sum_{k=0}^\infty\frac{A^k}{k!}\right) =e^Ae^B.$
$e^{i\alpha A}e^{i\beta A}=e^{i(\alpha+\beta)A}~,~~$where $\alpha,\beta\in\mathbb{R}.$
Proof: $~~~\because~[i\alpha A,i\beta A]=0~,~~ \therefore e^{i\alpha A}e^{i\beta A}=e^{i\alpha A+i\beta A}=e^{i(\alpha+\beta)A}.$
If $A$ is skew-Hermitian, i.e. $A^\dagger=-A,$ then $e^A$ is unitary.
Proof: $e^A(e^A)^\dagger=e^Ae^{A^\dagger}=e^{A+A^\dagger}=e^{A-A}=I.$
If $A$ is Hermitian, i.e. $A^\dagger=A,$ then $e^{i\alpha A}$ is unitary for any $\alpha\in\mathbb{R}$.
Proof: $e^{i\alpha A}(e^{i\alpha A})^\dagger=e^{i\alpha A}e^{(i\alpha A)^\dagger}=e^{i\alpha A-i\alpha A}=I.$
For diagonal matrix $D= \begin{bmatrix} d_1 & 0 & \cdots & 0\\ 0 & d_2 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & d_n \end{bmatrix} ,~~ e^D= \begin{bmatrix} e^{d_1} & 0 & \cdots & 0\\ 0 & e^{d_2} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & e^{d_n} \end{bmatrix} .$
$\displaystyle\frac{d}{dt}e^{tA} =\frac{d}{dt}I+\sum_{k=1}^\infty{1\over k!}A^k\frac{d}{dt}t^k =\sum_{k=1}^\infty{1\over k!}A^kkt^{k-1} =A\sum_{k=1}^\infty{1\over(k-1)!}A^{k-1}t^{k-1} =Ae^{tA} =e^{tA}A .$
Special Conditions¶
When $\displaystyle A^2=I,~~e^{i\theta A} =I\cos\theta+iA\sin\theta,~~$ where $\theta\in\mathbb{R}.$
Proof: $\displaystyle e^{i\theta A} =\sum_{k=0}^\infty{1\over (2k)!}(i\theta~A)^{2k}+\sum_{k=0}^\infty{1\over (2k+1)!}(i\theta~A)^{2k+1}\\ =I\sum_{k=0}^\infty{1\over (2k)!}(-1)^k\theta^{2k}+iA\sum_{k=0}^\infty{1\over (2k+1)!}(-1)^k\theta^{2k+1} =I\cos\theta+iA\sin\theta .$
When $P^2=P$ for $n\in\mathbb{N}$ and $n>1~,~~e^P=I+(e-1)P~~~$ (an idempotent projector).
Proof: $\displaystyle \because P^2=P,~~\therefore P^n=P,~~$and$~~ e^P =\sum_{k=0}^\infty{1\over k!}P^k =I+\sum_{k=1}^\infty{1\over k!}P =I+\left(\sum_{k=0}^\infty{1\over k!}-1\right)P =I+\left(e-1\right)P .$
Rotation¶
Generator $G\equiv\Ket b\Bra a-\Ket{a}\Bra{b}~,~~$where $\Ket a$ and $\Ket b$ are perpendicular unit vectors. i.e. $\Braket{a\Verti a}=1, \Braket{b\Verti b}=1,~$and$~\Braket{a\Verti b}=0.$
Projector $P\equiv\Ket{a}\Bra{a}+\Ket{b}\Bra{b}=-G^2~.$
We have $P^2=P$ and therefore $P^n=P,~~$and by observation$~~PG=GP=G.$
Operator to rotate angle $\theta$ from $\Ket{a}$ to $\Ket{b}$ (about the origin) is $\varpi(\theta)=e^{G\theta}.$
For $n\ge 1~,~~G^{2n}=(-1)^nP~,~~$and $G^{2n+1}=(-1)^nPG=(-1)^nG.$
$\varpi(\theta)=e^{G\theta}\\ =\sum_{k=0}^\infty{1\over k!}(G\theta)^k\\ =I+\sum_{k=1}^\infty{1\over(2k)!}(G\theta)^{2k}+G\theta+\sum_{k=1}^\infty{1\over(2k+1)!}(G\theta)^{2k+1}\\ =I+P\sum_{k=1}^\infty{\theta^{2k}\over(2k)!}(-1)^k+G\theta+\sum_{k=1}^\infty{\theta^{2k+1}\over(2k+1)!}(-1)^kPG\\ =I-P+P\sum_{k=0}^\infty{\theta^{2k}\over(2k)!}(-1)^k+G\sum_{k=0}^\infty{\theta^{2k+1}\over(2k+1)!}(-1)^k\\ =I-P+P\cos\theta+G\sin\theta .$
An observation: $P$ and $G$ is analogous to 1 and $i$ in many ways: $P=-G^2$ to $1=-i^2$, $P^2=P$ to $1^2=1$, $PG=GP=G$ to $1\times i=i\times 1=i$.
So $\varpi(\theta)=e^{G\theta}=I-P+P\cos\theta+G\sin\theta$ is like $e^{i\theta}=\cos\theta+i\sin\theta$, except that we have an extra $I-P$, which is like $1-1=0$ (sort of).
Notes¶
- The above rotation is an operator to rotate on a plane in the vector space spanned by $\Ket a$ to $\Ket b$.
These two vectors define the direction of rotation and are not the start-top points.
(They are orthogonal but $\theta$ is not necessarily $\pi/2$).
This rotation does not correspond rotation on the Bloch Sphere.
- The mapping between the vector space and the Bloch Sphere is not linear.
The same starting point on both systems may end up on different points after the rotation,
even when the "rotation speed" is compensated.
They simply follow different paths, except in special cases like with the Pauli axis.
- The choice of $\Ket a$ and $\Ket b$ is abitrary, as long as they are orthonormal
and the rotation is in the direction of $\Ket a$ to $\Ket b$.
(You would notice that by swapping $\Ket a$ and $\Ket b$ it only affects $G$ with a negative sign, which reverses the rotation direction, equivalent to rotating from the tail of $\Ket a$, or $-\Ket a$, to $\Ket b$.)
- In the exponent expressions discussed below, the negative sign is an intrinsic part of the exponent, not an indication of direction.
- The $\varpi_x, \varpi_y$ and $\varpi_z$ rotations by $\theta$ in this context are in the vector space, using the two "ends" of the Bloch Sphere as $\Ket a$ and $\Ket b$ as they are orthonormal. They corresponds to Bloch Rotation of $R_x, R_y$ and $R_z$ (but by half the rate).
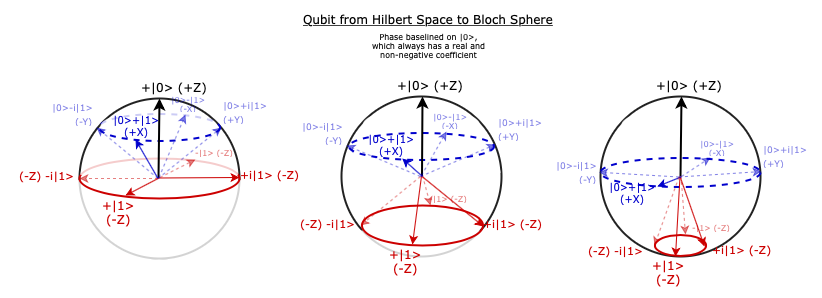
Note: In the discussion of Bloch Sphere Orthonormality, any two states at the two ends of a diameter of the Bloch Sphere are orthonomal. This is not generally true for the Hilbert Space presentation above. For example, $+\Ket1$ and $+i\Ket1$ are not orthonormal.
$R_x(\theta)$¶
$\varpi_x(\theta)$ rotation from $\Ket a=\Ket0$ to $\Ket b=-i\Ket1.$ Note $\Braket{a\Verti b}=\Braket{0\Verti 1}i=0.$
From the the Bloch Sphere representation, $\Ket0$ to $-i\Ket1$ is a $\pi$ rotation about $X$.
$G =\Ket b\Bra a-\Ket a\Bra b =-i\Ket1\Bra0-i\Ket0\Bra1 =\begin{bmatrix} 0 & -i\\ -i & 0 \end{bmatrix} .$
$P =\Ket a\Bra a+\Ket b\Bra b =\Ket0\Bra0+\Ket1\Bra1 =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} .$
$\varpi_x(\theta)=I-P+P\cos\theta+G\sin\theta =\begin{bmatrix} \cos\theta & -i\sin\theta\\ -i\sin\theta & \cos\theta \end{bmatrix} .$
Exponent $~e^{-i\theta X} =I\cos\theta-iX\sin\theta =\begin{bmatrix} \cos\theta & 0\\ 0 & \cos\theta \end{bmatrix} -i\begin{bmatrix} 0 & \sin\theta\\ \sin\theta & 0 \end{bmatrix} =\begin{bmatrix} \cos\theta & -i\sin\theta\\ -i\sin\theta & \cos\theta \end{bmatrix} .$
$\boxed{\varpi_x(\theta) =e^{-i\theta X} =\begin{bmatrix} \cos\theta & -i\sin\theta\\ -i\sin\theta & \cos\theta \end{bmatrix} }$ in the vector space.
Bloch Sphere $X$-axis rotation is also twice as fast as with orthonormal basis: $R_x(\theta)=\varpi_x(\theta/2).$
$\boxed{R_x(\theta) =e^{-i{\theta\over 2}X} =\begin{bmatrix} \cos{\theta\over 2} & -i\sin{\theta\over 2}\\ -i\sin{\theta\over 2} & \cos{\theta\over 2} \end{bmatrix} }$ on the Bloch Sphere.
Rotation by $\pi/2$ about the $X$-axis is $R_x(\pi/2)=\varpi_x(\pi/4) =\Rsr2\begin{bmatrix} 1 & -i\\ -i & 1 \end{bmatrix} .$
This sends $\Ket0$ to $\Rsr2(\Ket0-i\Ket1)~~$ and $~~\Ket1$ to $\Rsr2(-i\Ket0+\Ket1)\sim\Rsr2(\Ket0+i\Ket1).$
$R_y(\theta)$¶
$\varpi_y(\theta)$ rotates from $\Ket a=\Ket0$ to $\Ket b=\Ket1.$ Note $\Braket{a\Verti b}=\Braket{0\Verti 1}=0.$
From the the Bloch Sphere representation, $\Ket0$ to $\Ket1$ is a $\pi$ rotation about $Y$.
$G =\Ket b\Bra a-\Ket a\Bra b =\Ket1\Bra0-\Ket0\Bra1 =\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} .$
$P =\Ket a\Bra a+\Ket b\Bra b =\Ket0\Bra0+\Ket1\Bra1 =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} .$
$\varpi_y(\theta)=I-P+P\cos\theta+G\sin\theta =\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} .$
Exponent $~e^{-i\theta Y} =I\cos\theta-iY\sin\theta =\begin{bmatrix} \cos\theta & 0\\ 0 & \cos\theta \end{bmatrix} -i\begin{bmatrix} 0 & -i\sin\theta\\ i\sin\theta & 0 \end{bmatrix} =\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} .$
$\boxed{\varpi_y(\theta) =e^{-i\theta Y} =\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} }$ in the vector space.
Bloch Sphere $Y$-axis rotation is twice as fast as with orthonormal basis: $R_y(\theta)=\varpi_y(\theta/2).$
$\boxed{R_y(\theta) =e^{-i{\theta\over 2}Y} =\begin{bmatrix} \cos{\theta\over 2} & -\sin{\theta\over 2}\\ \sin{\theta\over 2} & \cos{\theta\over 2} \end{bmatrix} }$ on the Bloch Sphere.
Rotation by $\pi/2$ about the $Y$-axis is $R_y(\pi/2)=\varpi_y(\pi/4) =\Rsr2\begin{bmatrix} 1 & -1\\ 1 & 1 \end{bmatrix} .$
This sends $\Ket0$ to $\Rsr2(\Ket0+\Ket1)~~$ and $~~\Ket1$ to $\Rsr2(-\Ket0+\Ket1)\sim\Rsr2(\Ket0-\Ket1).$
Note: $R_y(\pi/2)$ is not a Hadamard operation, as it is not self-inverse (i.e. $(R_y(\pi/2))^2=R_y(\pi)\ne I.$)
$R_z(\theta)$¶
$\varpi_z(\theta)$ rotates from $\Ket a=\Rsr2(\Ket0+i\Ket1)$ to $\Ket b=\Rsr2(\Ket0-i\Ket1).$ Note $\Braket{a\Verti b} =\Rsr2(\Bra0-i\Bra1)\Rsr2(\Ket0-i\Ket1) ={1\over 2}(\Braket{0\Verti 0}-\Braket{1\Verti 1})=0.$
From the the Bloch Sphere representation, $\Rsr2(\Ket0+i\Ket1)$ to $\Rsr2(\Ket0-i\Ket1)$ is not an obvious $\pi$ rotation about $Z$. A $\pi$ rotation about $X$ can achieve the same result. We will discuss this apparant confusion by rotating a $\pi/2$ on Bloch Sphere at the end of this section.
$G =\Ket b\Bra a-\Ket a\Bra b =\Rsr2(\Ket0-i\Ket1)\Rsr2(\Bra0-i\Bra1)-\Rsr2(\Ket0+i\Ket1)\Rsr2(\Bra0+i\Bra1)\\ ={1\over 2}(\Ket0\Bra0-i\Ket0\Bra1-i\Ket1\Bra0-\Ket1\Bra1) -{1\over 2}(\Ket0\Bra0+i\Ket0\Bra1+i\Ket1\Bra0-\Ket1\Bra1) =\begin{bmatrix} 0 & -i\\ -i & 0 \end{bmatrix} .$
$P =\Ket a\Bra a+\Ket b\Bra b =\Rsr2(\Ket0+i\Ket1)\Rsr2(\Bra0-i\Bra1)+\Rsr2(\Ket0-i\Ket1)\Rsr2(\Bra0+i\Bra1)\\ ={1\over 2}(\Ket0\Bra0-i\Ket0\Bra1+i\Ket1\Bra0+\Ket1\Bra1) +{1\over 2}(\Ket0\Bra0+i\Ket0\Bra1-i\Ket1\Bra0+\Ket1\Bra1) =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} .$
$\varpi_z(\theta)=I-P+P\cos\theta+G\sin\theta =\begin{bmatrix} \cos\theta-i\sin\theta & 0\\ 0 & \cos\theta+i\sin\theta \end{bmatrix} =\begin{bmatrix} e^{-i\theta} & 0\\ 0 & e^{i\theta} \end{bmatrix} .$
Exponent $~e^{-i\theta Z} =I\cos\theta-iZ\sin\theta =\begin{bmatrix} \cos\theta & 0\\ 0 & \cos\theta \end{bmatrix} -i\begin{bmatrix} \sin\theta & 0\\ 0 & -\sin\theta \end{bmatrix} =\begin{bmatrix} \cos\theta-i\sin\theta & 0\\ 0 & \cos{\theta}+i\sin\theta \end{bmatrix} =\begin{bmatrix} e^{-i\theta} & 0\\ 0 & e^{i\theta} \end{bmatrix} .$
$\boxed{\varpi_z(\theta) =e^{-i\theta Z} =\begin{bmatrix} e^{-i\theta} & 0\\ 0 & e^{i\theta} \end{bmatrix} }$ in the vector space.
Bloch Sphere $Z$-axis rotation is twice as fast as with orthonormal basis: $R_z(\theta)=\varpi_z(\theta/2).$
$\boxed{R_z(\theta) =e^{-i{\theta\over 2}Z} =\begin{bmatrix} e^{-i\theta/2} & 0\\ 0 & e^{i\theta/2} \end{bmatrix} }$ on the Bloch Sphere.
Rotation by $\pi/2$ about the $Z$-axis is $R_z(\pi/2)=\varpi_z(\pi/4) =\begin{bmatrix} e^{-i\pi/4} & 0\\ 0 & e^{i\pi/4} \end{bmatrix} \sim\begin{bmatrix} 1 & 0\\ 0 & e^{i\pi/2} \end{bmatrix} =\begin{bmatrix} 1 & 0\\ 0 & i \end{bmatrix} .$
This sends $\Rsr2(\Ket0+\Ket1)$ to $\Rsr2(\Ket0+i\Ket1)~~$ and $~~\Rsr2(\Ket0-\Ket1)$ to $\Rsr2(\Ket0-i\Ket1).$
Discussion on $Z$ rotation¶
As stated earlier, rotating from $\Rsr2(\Ket0+i\Ket1)$ to $\Rsr2(\Ket0-i\Ket1)$ can be achieved by either a $R_x(\pi)$ or $R_z(\pi)$ operation.
However, $R_x(\pi/2)\Rsr2(\Ket0+i\Ket1)$ gives you $\Ket0$, while $R_z(\pi/2)\Rsr2(\Ket0+i\Ket1)$ gives you $\Rsr2(\Ket0-\Ket1)$.
Now, if we rotate from $\Ket a=\Rsr2(\Ket0+\Ket1)$ to $\Ket b=\Rsr2(\Ket0-\Ket1)$, $\varpi'_z(\theta) =\begin{bmatrix} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{bmatrix} ,$ as illustrated in the following.
$G =\Ket b\Bra a-\Ket a\Bra b =\Rsr2(\Ket0-\Ket1)\Rsr2(\Bra0+\Bra1)-\Rsr2(\Ket0+\Ket1)\Rsr2(\Bra0-\Bra1)\\ ={1\over 2}(\Ket0\Bra0+\Ket0\Bra1-\Ket1\Bra0-\Ket1\Bra1) -{1\over 2}(\Ket0\Bra0-\Ket0\Bra1+\Ket1\Bra0-\Ket1\Bra1) =\begin{bmatrix} 0 & 1\\ -1 & 0 \end{bmatrix} .$
$P =\Ket a\Bra a+\Ket b\Bra b =\Rsr2(\Ket0+\Ket1)\Rsr2(\Bra0+\Bra1)+\Rsr2(\Ket0-\Ket1)\Rsr2(\Bra0-\Bra1)\\ ={1\over 2}(\Ket0\Bra0+\Ket0\Bra1+\Ket1\Bra0+\Ket1\Bra1) +{1\over 2}(\Ket0\Bra0-\Ket0\Bra1-\Ket1\Bra0+\Ket1\Bra1) =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} .$
$\varpi_z(\theta)=I-P+P\cos\theta+G\sin\theta =\begin{bmatrix} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{bmatrix} .$
Rotation by $\pi/2$ about the some axis $\phi$ is $R_\phi(\pi/2) =\varpi'_z(\pi/4) =\Rsr2\begin{bmatrix} 1 & 1\\ -1 & 1 \end{bmatrix} =ZH\sim\sqrt{Y}.$
$ZH=\Rsr2\begin{bmatrix}1&1\\-1&1\end{bmatrix}, ZHZH=\frac{1}{2}\begin{bmatrix}1&1\\-1&1\end{bmatrix}\begin{bmatrix}1&1\\-1&1\end{bmatrix}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}\sim Y .$